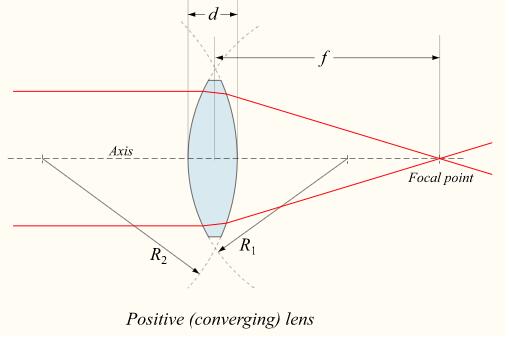
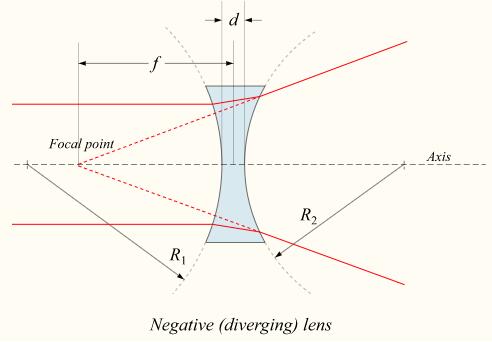
Lenses are classified by the curvature of the two optical surfaces. A lens is biconvex (or double convex, or just convex) if both surfaces are convex. If both surfaces have the same radius of curvature, the lens is equiconvex. A lens with two concave surfaces is biconcave (or just concave). If one of the surfaces is flat, the lens is plano-convex or plano-concave depending on the curvature of the other surface. A lens with one convex and one concave side is convex-concave or meniscus. It is this type of lens that is most commonly used in corrective lenses, since its shape minimizes some aberrations. If the lens is biconvex or plano-convex, a collimated beam of light passing through the lens converges to a spot (a focus) behind the lens. In this case, the lens is called a positive or converging lens. For a thin lens in air, the distance from the lens to the spot is the focal length of the lens, which is commonly represented by f in diagrams and equations. An extended hemispherical lens is a special type of plano-convex lens, in which the lens's curved surface is a full hemisphere and the lens is much thicker than the radius of curvature.
A lens is a transmissive optical device that focuses or disperses a light beam by means of refraction. A simple lens consists of a single piece of transparent material, while a compound lens consists of several simple lenses (elements), usually arranged along a common axis. Lenses are made from materials such as glass or plastic and are ground, polished, or molded to the required shape. A lens can focus light to form an image, unlike a prism, which refracts light without focusing. Devices that similarly focus or disperse waves and radiation other than visible light are also called "lenses", such as microwave lenses, electron lenses, acoustic lenses, or explosive lenses.
Lenses are used in various imaging devices such as telescopes, binoculars, and cameras. They are also used as visual aids in glasses to correct defects of vision such as myopia and hypermetropia.
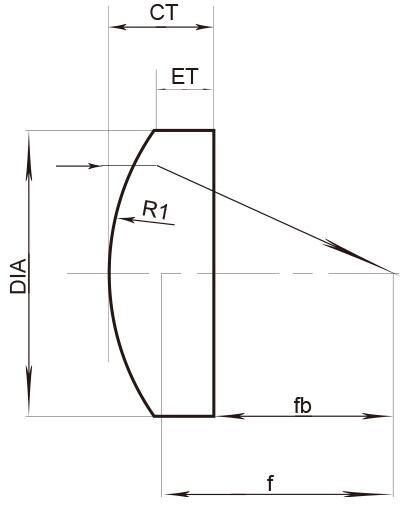
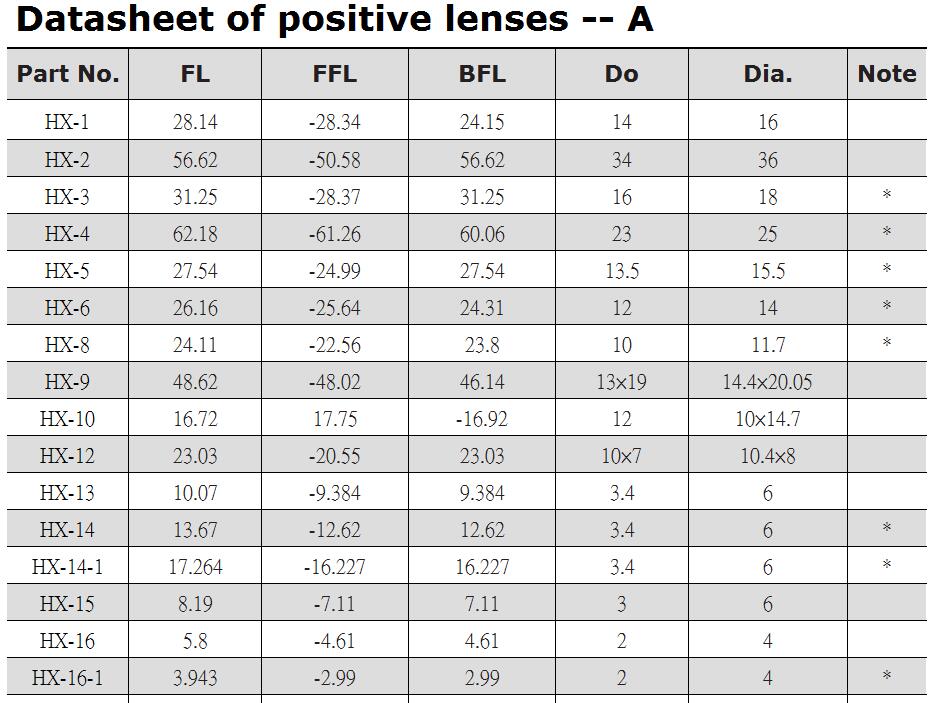
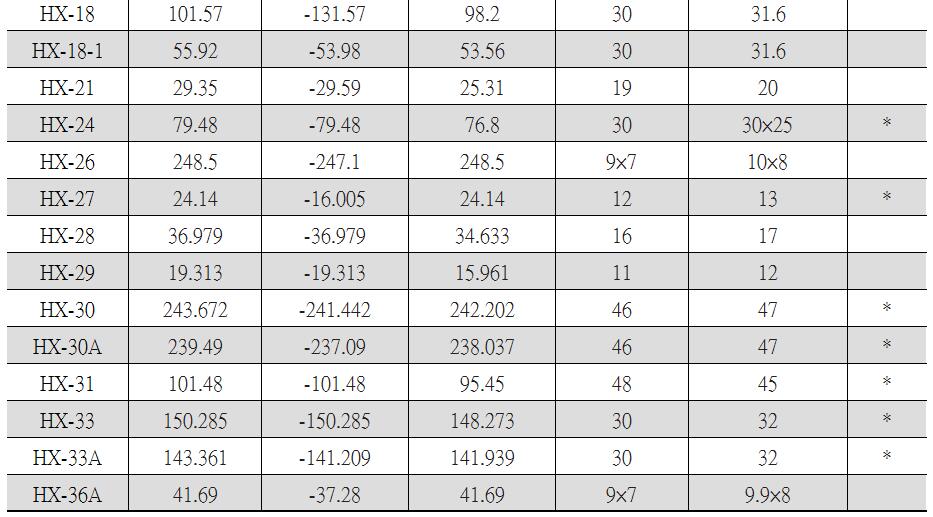
Dia.=diameter ; Do= Inside diameter ; FL= focal length
BFL= Back of focus ; CT= Center Thickness ; ET = Edge Thickness
Surface profile:
While in principle aspheric surfaces can take a wide variety of forms, aspheric lenses are often designed with surfaces of the form
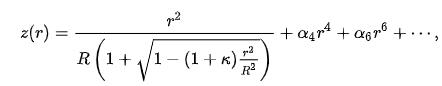
where the optic axis is presumed to lie in the z direction, and z(r) is the sag—the z-component of the displacement of the surface from the vertex, at distance
r from the axis. The coefficients alpha;describe the deviation of the surface from the axially symmetric quadric surface specified by R and kappa .
If the coefficients alpha are all zero, then R is the radius of curvature and kappa is the conic constant, as measured at the vertex (where r=0). In this case, the surface has the form of a conic section rotated about the optic axis, with form determined by kappa :

The above equation suffers from strong correlation between the coefficients of the first term and the polynomial terms. This leads to strong divergences when it comes to fitting the equation to an aspheric surface. Therefore, different equations using "Q-polynomials" where coefficients are orthogonal to each other are an alternative that is sometimes used.