Product Catalog
Hot Product

Product

Aspheric Plano-Convex(PCX) Zoom Lighting,Stage lighting Optical Lenses Series

Plano-Convex (PCX) Lenses have a positive focal length, making them ideal for collecting and focusing light in imaging applications. They are also useful in a variety of applications involving emitters, detectors, lasers, and fiber optics. Coated versions have optimum light transmission. Available in a wide variety of diameters and focal lengths. Plano-Concave (PCV) lenses have one flat and one inward curved surface. PCV lenses have a negative focal length and are used for image reduction or to spread light. Double-Convex (DCX) Lenses have two outward curved surfaces, a positive focal length and are useful for 1:1 imaging and in multi-element systems. Double-Concave (DCV) Lenses have two inward curved surfaces and a negative focal length. They are used for image reduction and to spread light. Meniscus lenses are convex-concave lenses. They have one outward curved face and one inward-curved face. If the outward curve is sharper than the inward curve, the lens has a positive focal length and acts as a magnifier.


Product Description

A zoom lens is a system of camera lens elements for which the focal length (and thus angle of view) can be varied, as opposed to a fixed-focal-length (FFL) lens (prime lens). A true zoom lens or optical zoom lens is a type of parfocal lens, one that maintains focus when its focal length changes.[1] Most consumer zoom lenses do not maintain perfect focus, but are still nearly parfocal. Most camera phones that are advertised as having optical zoom actually use a few cameras of different but fixed focal length, combined with digital zoom to make a hybrid system.

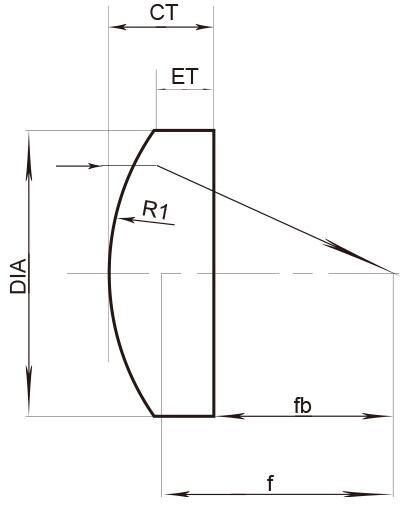
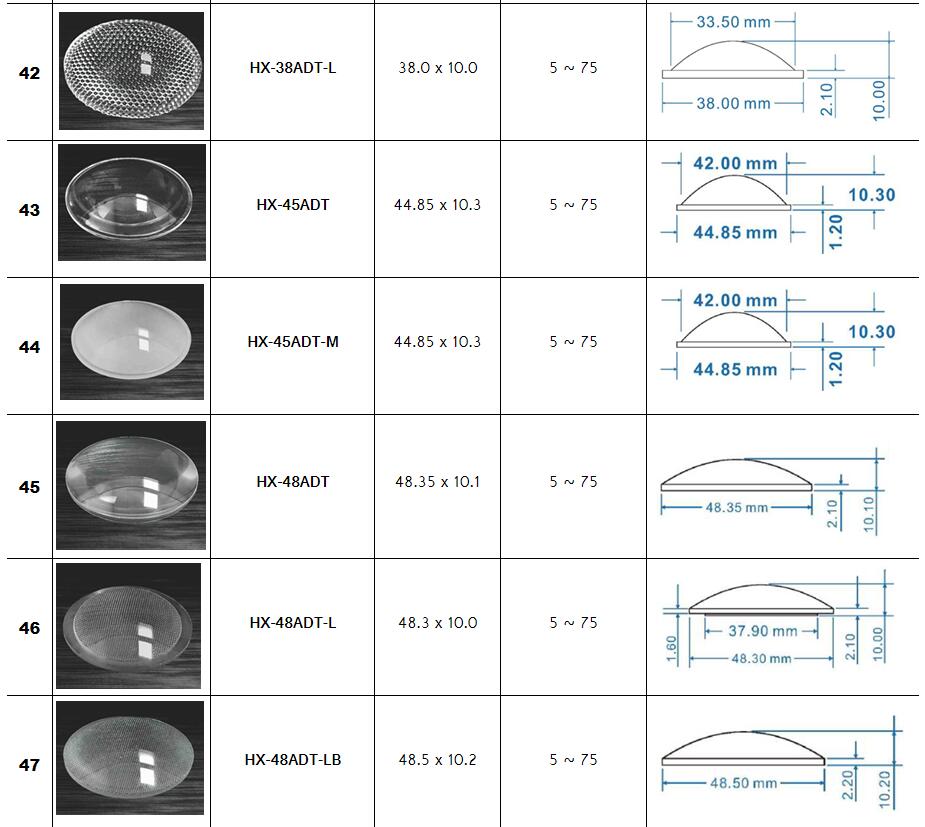
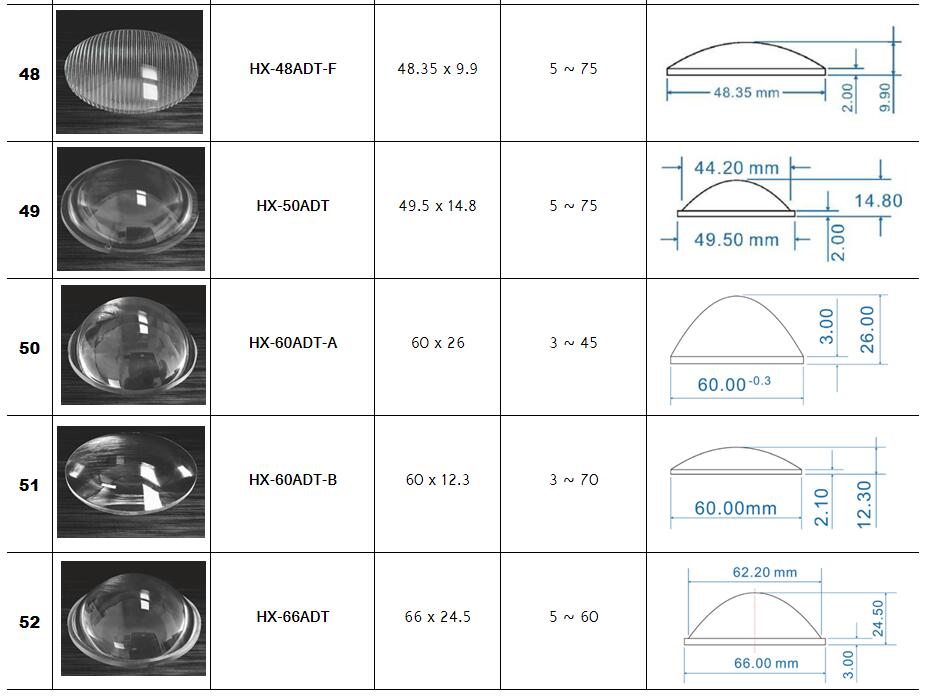
Dia.=diameter ; Do= Inside diameter ; FL= focal length
BFL= Back of focus ; CT= Center Thickness ; ET = Edge Thickness


Zoom Lighting,Stage lighting Optical Lenses Series :


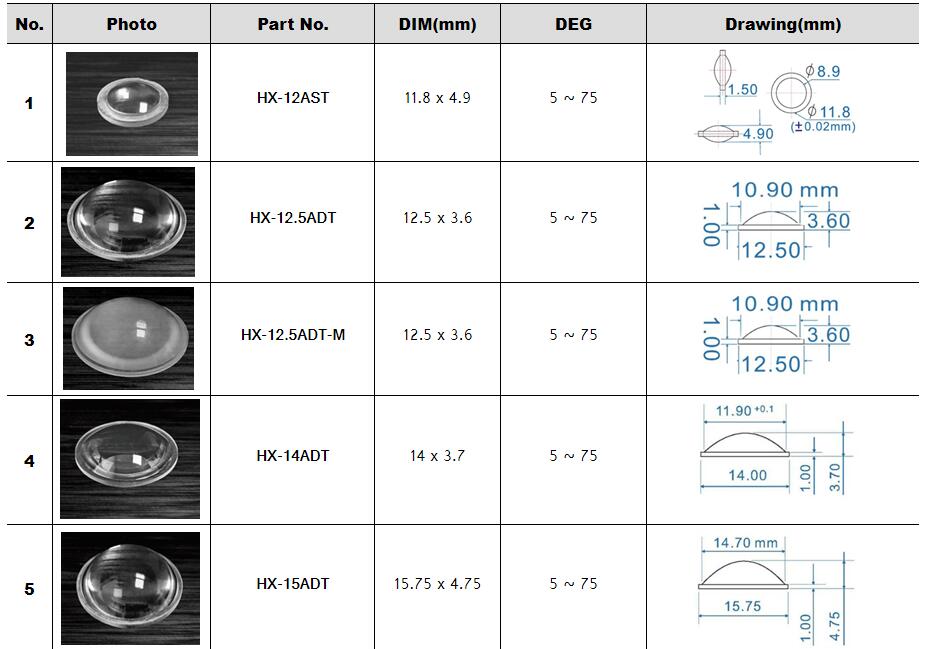
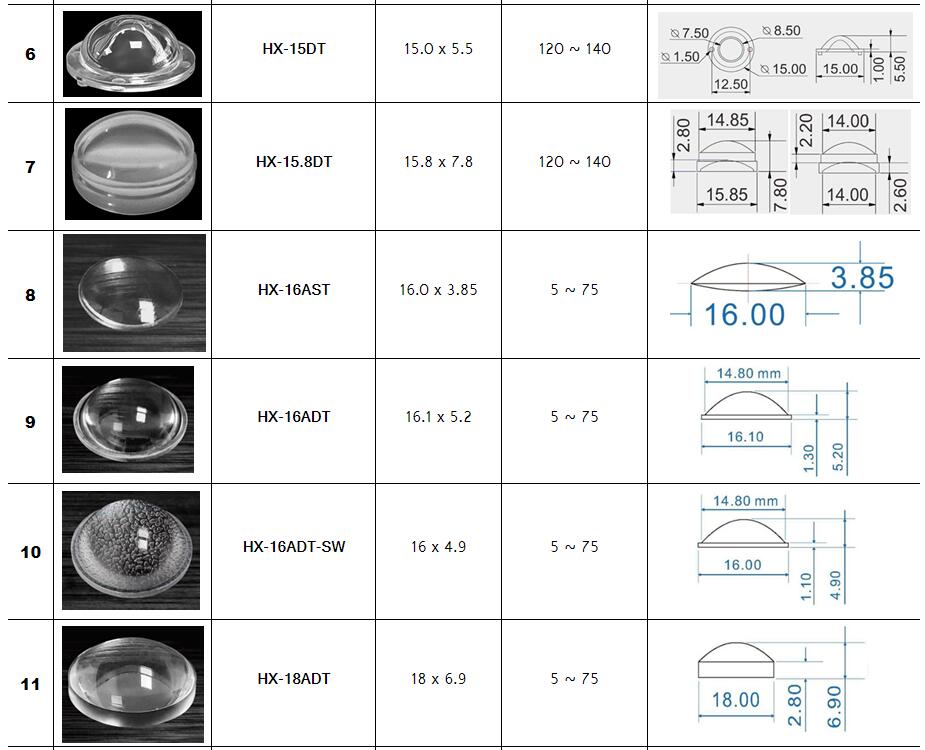
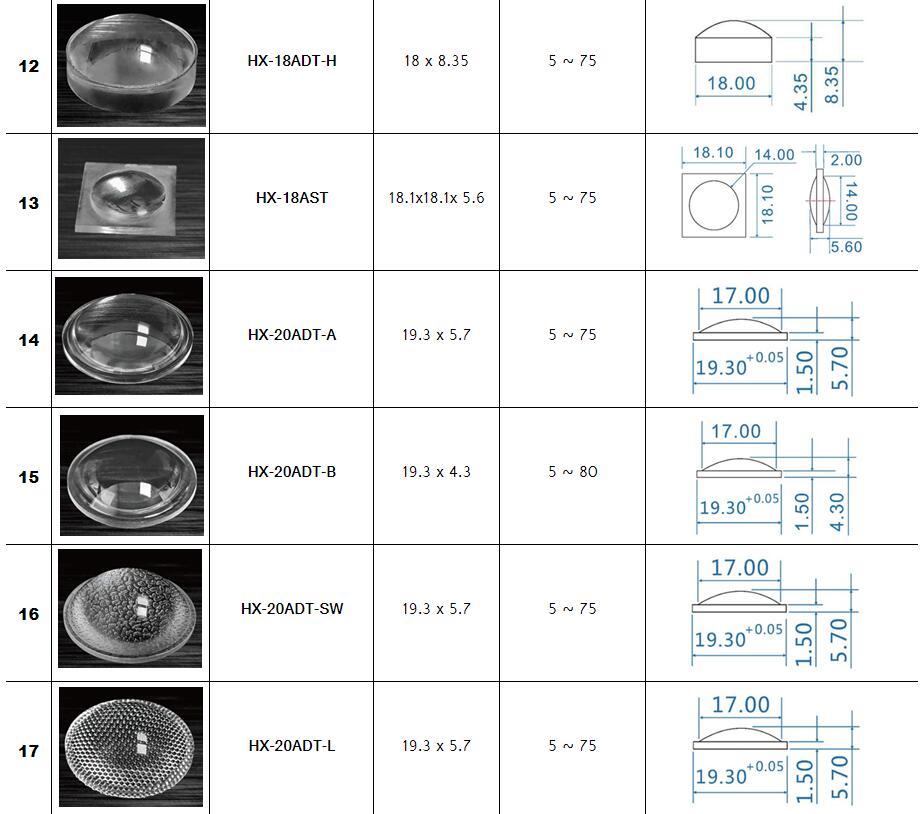
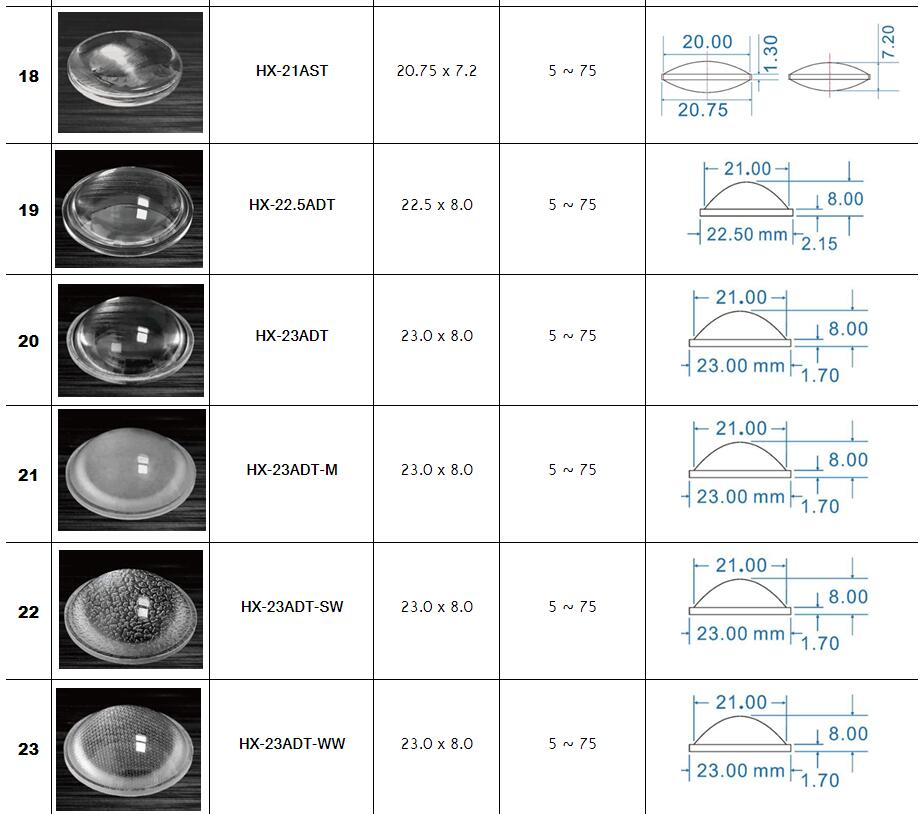
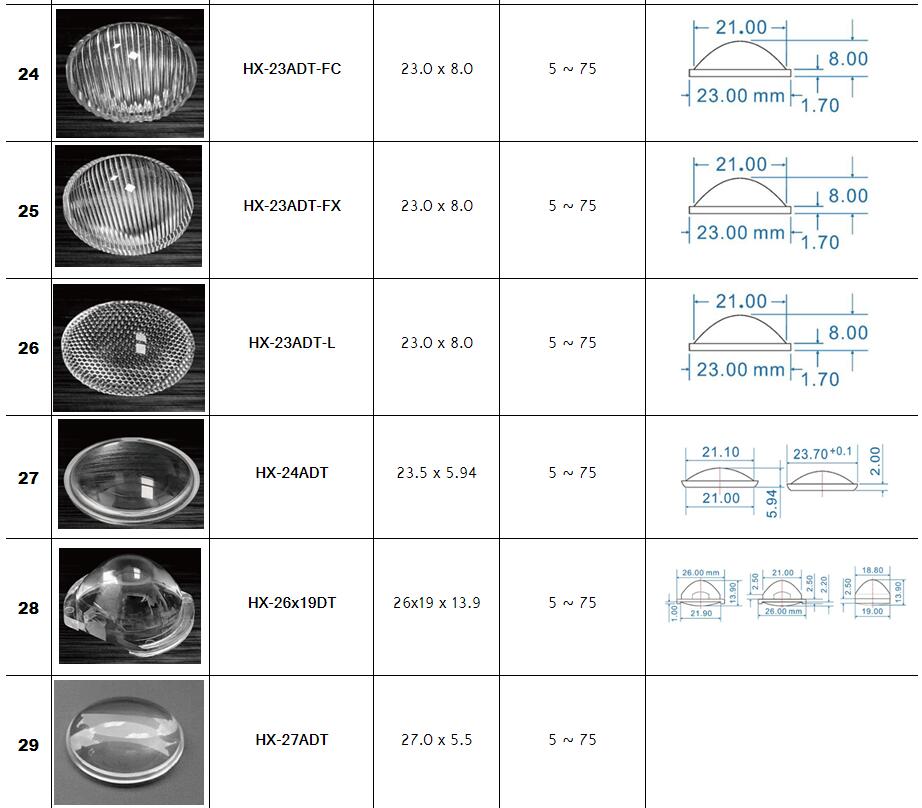
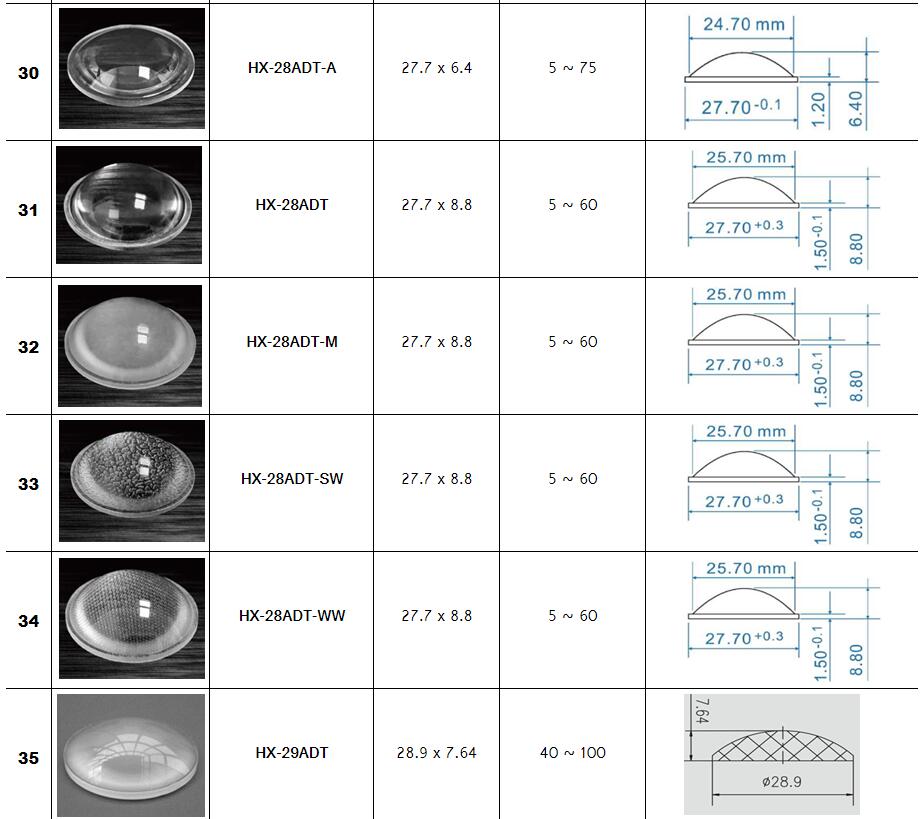
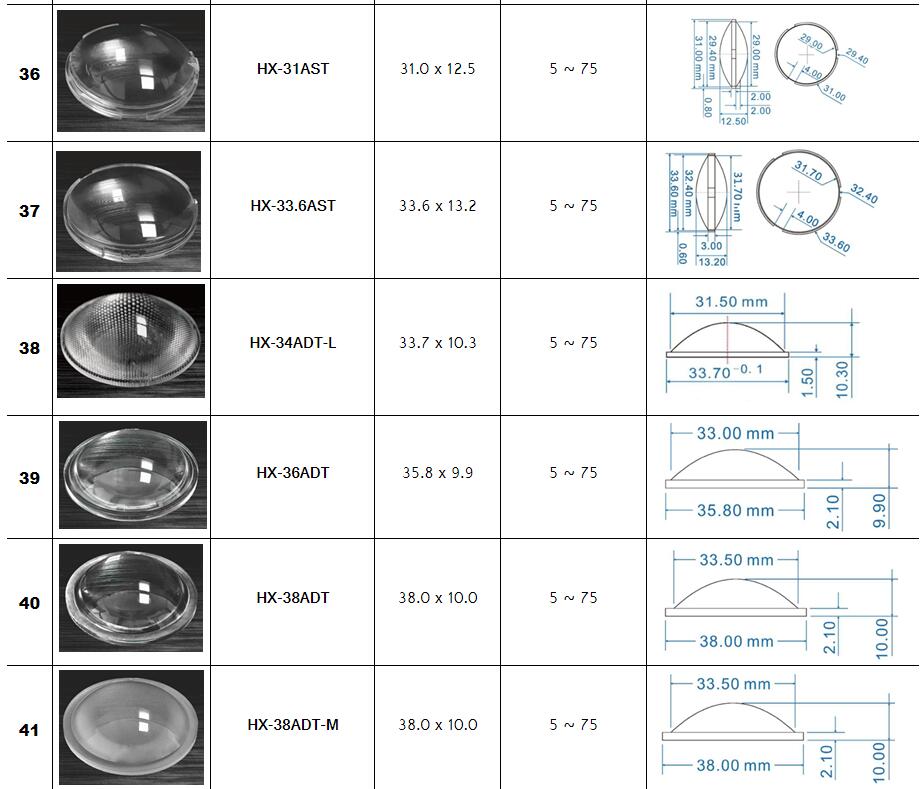
Surface profile:
While in principle aspheric surfaces can take a wide variety of forms, aspheric lenses are often designed with surfaces of the form



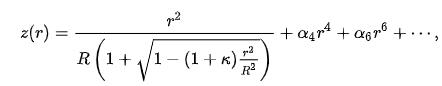
where the optic axis is presumed to lie in the z direction, and z(r) is the sag—the z-component of the displacement of the surface from the vertex, at distance r from the axis. The coefficients alpha;describe the deviation of the surface from the axially symmetric quadric surface specified by R and kappa . If the coefficients alpha are all zero, then R is the radius of curvature and kappa is the conic constant, as measured at the vertex (where r=0). In this case, the surface has the form of a conic section rotated about the optic axis, with form determined by kappa :


The above equation suffers from strong correlation between the coefficients of the first term and the polynomial terms. This leads to strong divergences when it comes to fitting the equation to an aspheric surface. Therefore, different equations using "Q-polynomials" where coefficients are orthogonal to each other are an alternative that is sometimes used.

Product Download

Product Application

Stage lighting has multiple functions, including: Selective visibility: The ability to see what is occurring on stage. Any lighting design will be ineffective if the viewers cannot see the characters, unless this is the explicit intent. Revelation of form: Altering the perception of shapes onstage, particularly three-dimensional stage elements. Focus: Directing the audience's attention to an area of the stage or distracting them from another. Mood: Setting the tone of a scene. Harsh red light has a different effect than soft lavender light. Location and time of day: Establishing or altering position in time and space. Blues can suggest night time while orange and red can suggest a sunrise or sunset. Use of mechanical filters ("gobos") to project sky scenes, the Moon, etc. Projection/stage elements: Lighting may be used to project scenery or to act as scenery onstage. Plot (script): A lighting event may trigger or advance the action onstage and off. Composition: Lighting may be used to show only the areas of the stage which the designer wants the audience to see, and to "paint a picture".[4][5] Effect: In pop and rock concerts or DJ shows or raves, colored lights and lasers may be used as a visual effect. Lighting design is an art form, and thus no one way is the "correct" way. There is a modern movement that states that the lighting design helps to create the environment in which the action takes place while supporting the style of the piece. "Mood" is arguable while the environment is essential.[6]

Color temperature is measured in kelvins. A light's apparent color is determined by its lamp color, the color of any gels in the optical path, its power level, and the color of the material it lights.[7] A tungsten lamp's color is typically controlled by inserting one or more gels (filters) into its optical path. In the simplest case, a single gel is inserted into the optical path to produce light of the same color. For example, a blue gel is used to create blue light. Custom colors are obtained by means of subtractive CMY color mixing, by inserting combinations of cyan, magenta and yellow filters into the optical path of the lighting fixture. The inserted filters may have varying densities, with correspondingly varied percentages of transmission, that subtractively mix colors (the filters absorb unwanted light colors, but the desired colors pass through unaffected). Manufacturers will sometimes include an additional green or amber ("CTO" color correction) filter to extend the range (gamut) of subtractive color mixing systems. Lamp power also influences color in tungsten lamps. As the lamp power is decreased, the tungsten filament in a bulb will tend to produce increasing percentages of orange light, as compared to the nearly white light emitted at full power. This is known as amber shift or amber drift. Thus a 1000-watt instrument at 50 percent power will emit a higher percentage of orange light than a 500-watt instrument operating at full power.[8] LED fixtures create color through additive color mixing with red, green, blue, and in some cases amber, LEDs at different intensities. This type of color mixing is often used with borderlights and cyclorama lights.[9]

Stage lighting is the craft of lighting as it applies to the production of theater, dance, opera, and other performance arts.[1] Several different types of stage lighting instruments are used in this discipline.[2] In addition to basic lighting, modern stage lighting can also include special effects, such as lasers and fog machines. People who work on stage lighting are commonly referred to as lighting technicians or lighting designers. The equipment used for stage lighting (e.g. cabling, dimmers, lighting instruments, controllers) are also used in other lighting applications, including corporate events, concerts, trade shows, broadcast television, film production, photographic studios, and other types of live events. The personnel needed to install, operate, and control the equipment also cross over into these different areas of "stage lighting" applications.

Other Product